基本邏輯名詞 |
2009/02/25 ~ 阿亮 ~ |
|
最近看到一些簡單的邏輯 (Logic) 英詞名詞,並不是很清楚,所以,找出來再複習一下。
其實大部份是很簡單的,只是換成英文就不熟了.
Rules of Inference
|
Modus Ponens
|
Modus Tollens
|
Hypothetical Syllogism
|
|
Disjunctive Syllogism
|
Constructive Dilemma
|
Absorption
|
|
Simplification
|
Conjunction
|
Addition
|
Rules of Replacement
| Double Negation |  |
| Commutation |  |
| Tautology | 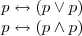 |
| Association |
|
| Transposition | 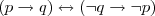 |
| Material Implication |  |
| Exportation | ![\begin{array}{l} \\ \left[(p\wedge q)\rightarrow r }\right] \leftrightarrow \left[p\rightarrow (q\rightarrow r)\right] \\ \end{array} \begin{array}{l} \\ \left[(p\wedge q)\rightarrow r }\right] \leftrightarrow \left[p\rightarrow (q\rightarrow r)\right] \\ \end{array}](https://derjohng.doitwell.tw/wp-content/plugins/dj-latexrender/pictures/dd2b117d1af69308a34e7f3ab70cc060.png) |
| Material Equivalence |
|
| Distribution |
|
| De Morgan’s Theorems |
|
Bi-conditionals Logical Equivalence
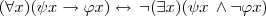
"Everything in the lake is wet."
is logically equivalent to
"There isn’t anything in the lake which is not wet."

"There exists at least one individual who is both a native of Boston and of Irish descent."
is logically equivalent to
"It’s not true that no natives of Boston are of Irish descent."

"No residents of Boston are Irish."
is logically equivalent to
"It’s not true that some residents of Boston are Irish."
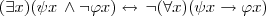
"Some residents of Boston are not Irish."
is logically equivalent to
"Not all residents of Boston are Irish."

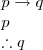
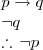
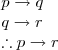
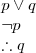
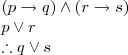
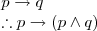
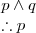
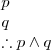
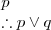
![\begin{array}{l} \\ \left[p\vee (q\vee r)\right] \leftrightarrow \left[(p\vee q)\vee r\right] \\ \left[p\wedge (q\wedge r)\right] \leftrightarrow \left[(p\wedge q)\wedge r\right] \\ \end{array} \begin{array}{l} \\ \left[p\vee (q\vee r)\right] \leftrightarrow \left[(p\vee q)\vee r\right] \\ \left[p\wedge (q\wedge r)\right] \leftrightarrow \left[(p\wedge q)\wedge r\right] \\ \end{array}](https://derjohng.doitwell.tw/wp-content/plugins/dj-latexrender/pictures/1171c17ed616046cb51c41b697f7a471.png)
![\begin{array}{l} \\
(p\leftrightarrow q)\leftrightarrow \left[(p\rightarrow q) \wedge (q\rightarrow p)\right] \\
(p\leftrightarrow q)\leftrightarrow \left[(p\wedge q) \vee (\neg p \,\wedge \neg q)\right] \\
\end{array} \begin{array}{l} \\
(p\leftrightarrow q)\leftrightarrow \left[(p\rightarrow q) \wedge (q\rightarrow p)\right] \\
(p\leftrightarrow q)\leftrightarrow \left[(p\wedge q) \vee (\neg p \,\wedge \neg q)\right] \\
\end{array}](https://derjohng.doitwell.tw/wp-content/plugins/dj-latexrender/pictures/968c0d5fbefc846a49e0e9b1a15dc4c8.png)
![\begin{array}{l} \\
\left[p \wedge (q\vee r)\left] \leftrightarrow \left[(p\wedge q)\vee (p\wedge r)\right] \\
\left[p \vee (q\wedge r)\left] \leftrightarrow \left[(p\vee q)\wedge (p\vee r)\right] \\
\end{array} \begin{array}{l} \\
\left[p \wedge (q\vee r)\left] \leftrightarrow \left[(p\wedge q)\vee (p\wedge r)\right] \\
\left[p \vee (q\wedge r)\left] \leftrightarrow \left[(p\vee q)\wedge (p\vee r)\right] \\
\end{array}](https://derjohng.doitwell.tw/wp-content/plugins/dj-latexrender/pictures/10e23ff9b260de555d2c35e6e45d4c6a.png)